Particle-antiparticle duality and fractionalization of topological chiral solitons
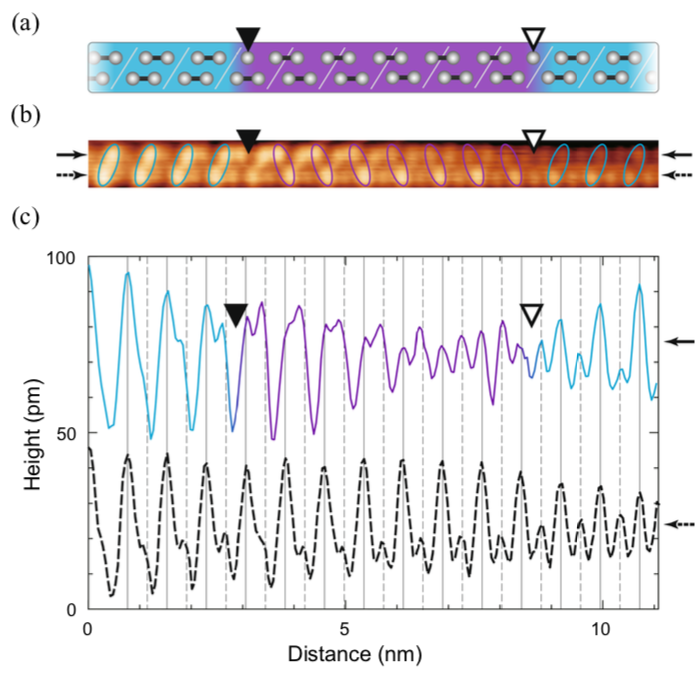
Although a prototypical Su–Schrieffer–Heeger (SSH) soliton exhibits various important topological concepts including particle-antiparticle (PA) symmetry and fractional fermion charges, there have been only few advances in exploring such properties of topological solitons beyond the SSH model. Here, by considering a chirally extended double-Peierls-chain model, we demonstrate novel PA duality and fractional charge e/2 of topological chiral solitons even under the chiral symmetry breaking. This provides a counterexample to the belief that chiral symmetry is necessary for such PA relation and fractionalization of topological solitons in a time-reversal invariant topological system. Furthermore, we discover that topological chiral solitons are re-fractionalized into two subsolitons which also satisfy the PA duality. As a result, such dualities and fractionalizations support the topological ℤ4 algebraic structures. Our findings will inspire researches seeking feasible and promising topological systems, which may lead to new practical applications such as solitronics.