Topological features of ground states and topological solitons in generalized Su-Schrieffer-Heeger models using generalized time-reversal, particle-hole, and chiral symmetries
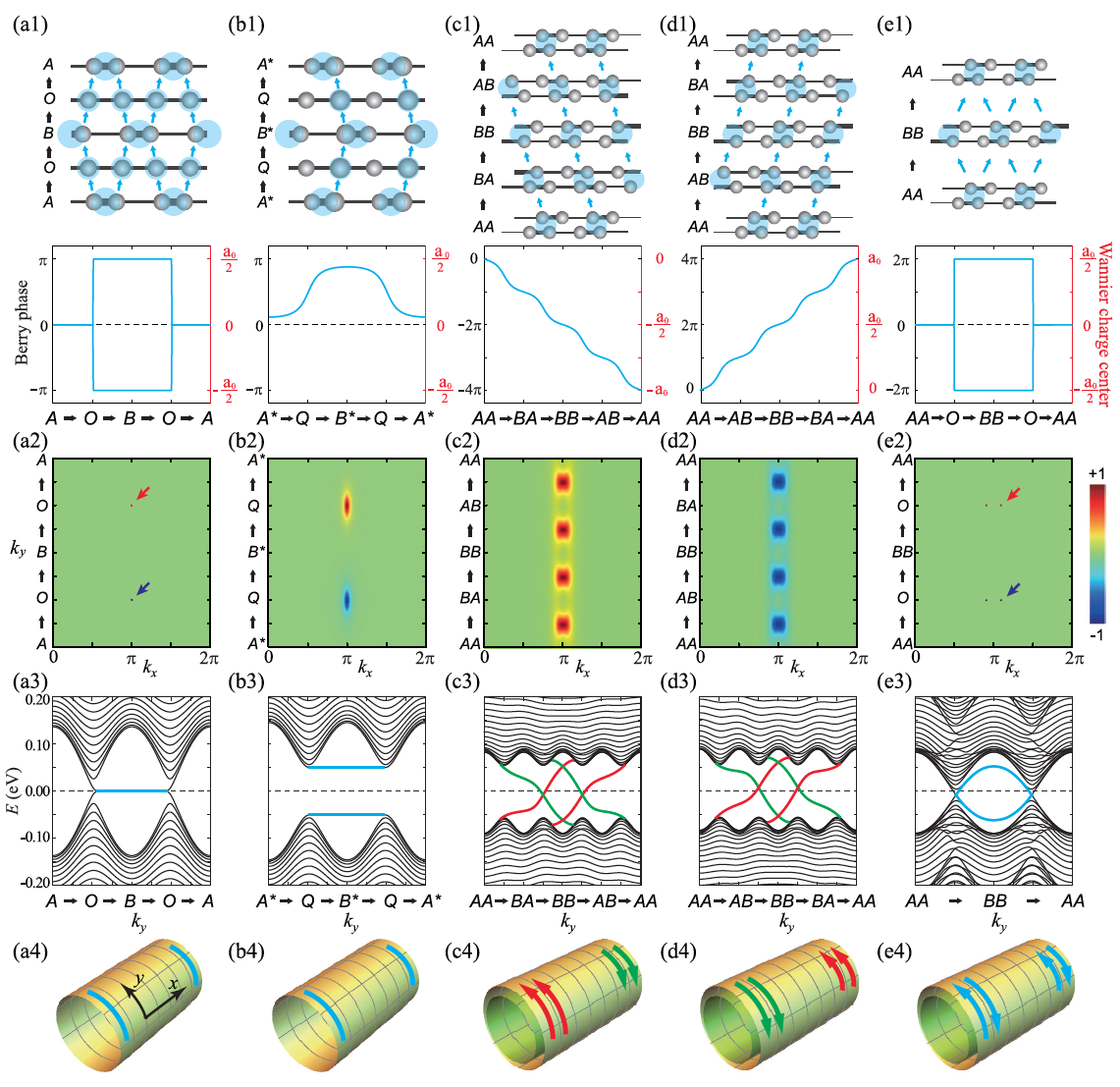
Topological phases and their topological features are enriched by the fundamental time-reversal, particle-hole, and chiral as well as crystalline symmetries. While one-dimensional (1D) generalized Su-Schrieffer-Heeger (SSH) systems show various topological phenomena such as topological solitons and topological charge pumping, it remains unclear how such symmetry protects and relates such topological phenomena. Here we show that the generalized time-reversal, particle-hole, and chiral symmetry operators consistently explain not only the symmetry transformation properties between the ground states but also the topological features of the topological solitons in prototypical quasi-1D systems such as the SSH, Rice-Mele, and double-chain models. As a consequence, we classify generalized essential operators into three groups: Class I and class II operators connect ground states in between after spontaneous symmetry breaking while class III operators give the generalized particle-hole and chiral symmetries to ground states. Furthermore, class I operators endow the equivalence relation between topological solitons while class II and III operators do the particle-hole relations. Finally, we demonstrate three distinct types of topological charge pumping and soliton chirality from the viewpoint of class I, II, and III operators. We build a general framework to explore the topological features of the generalized 1D electronic system, which can be easily applied in various condensed matter systems as well as photonic crystal and cold atomic systems.